DEBtox Researc


What is GUTS?

GUTS stands for "General Unified Threshold model for Survival". In other words, a modelling framework for the analysis of toxicity tests for the endpoint "survival". The method is expertly suited to analyse the results of standard acute toxicity tests (such as the 4-day test with fish, and the 2-day test with Daphnia). The "unified" relates to the fact that almost all models for the analysis of survival data can be seen as special cases within the GUTS framework. More background on GUTS. The simplest special case of GUTS was included into OECD and ISO guidances as early as 2006, under the denominator "biology-based methods". Download the OECD guidance.
 
GUTS thus replaces the standard dose-response analyses that are used to calculate an LC50. Advantages of a GUTS analysis:
  • Model parameters are estimated using all data points (for all treatments and all time points simultaneously). This implies more confidence, but also that data can be analysed that otherwise would need to be discarded (e.g., when there is no treatment with partial mortality at the end of the test).
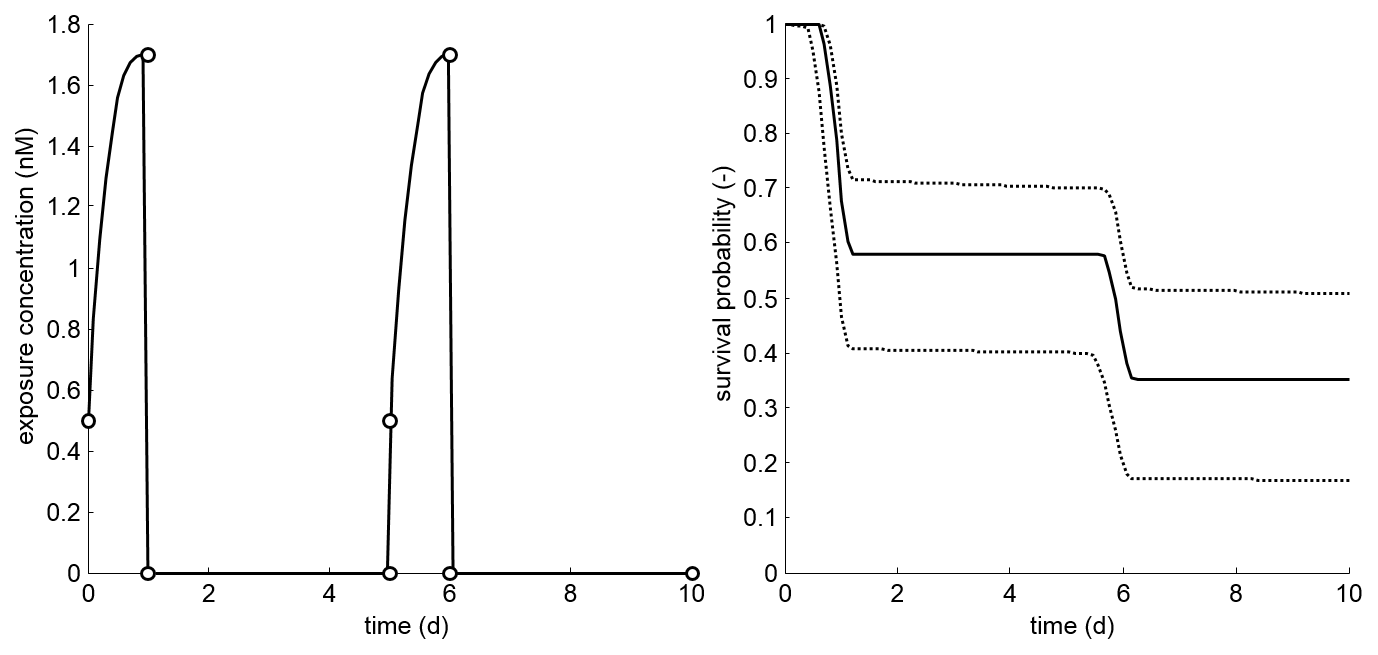
  • Time-varying exposure during the test can easily be accommodated, as long as the exposure profile is known (or can be estimated reliably). So, there is no strict need for constant exposures.
  • No problem when the animals grow (or shrink) during the test, as long as the amount of growth (or shrinking) is determined (or can be reliably estimated).
  • No problem when animals disappear from the test without dying from the test chemical (e.g., animals that escape, clear errors in handling, removal of animals during the test for destructive analyses). The information that the animals were still alive at a certain timepoint can be weighed into the analysis.
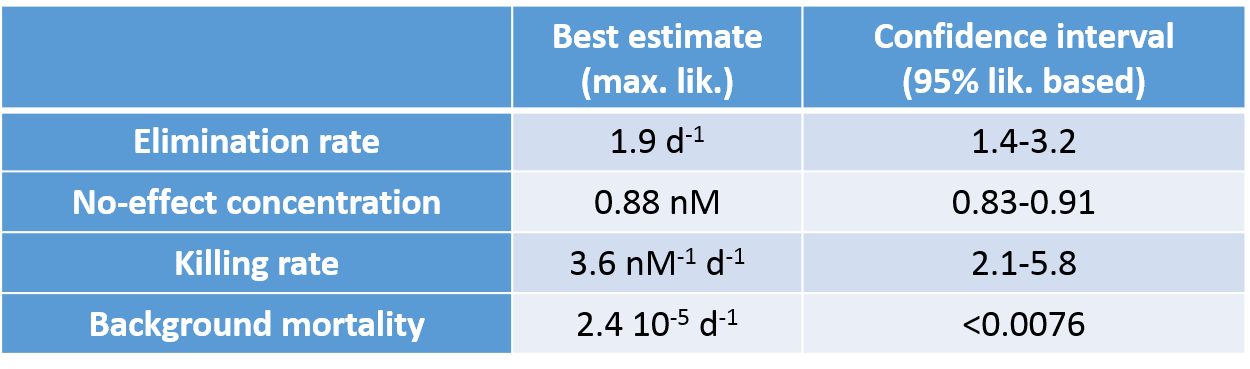
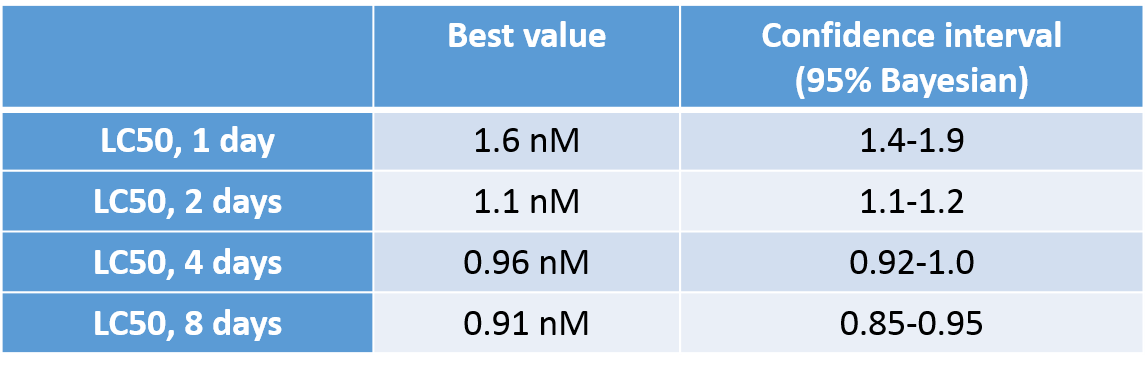
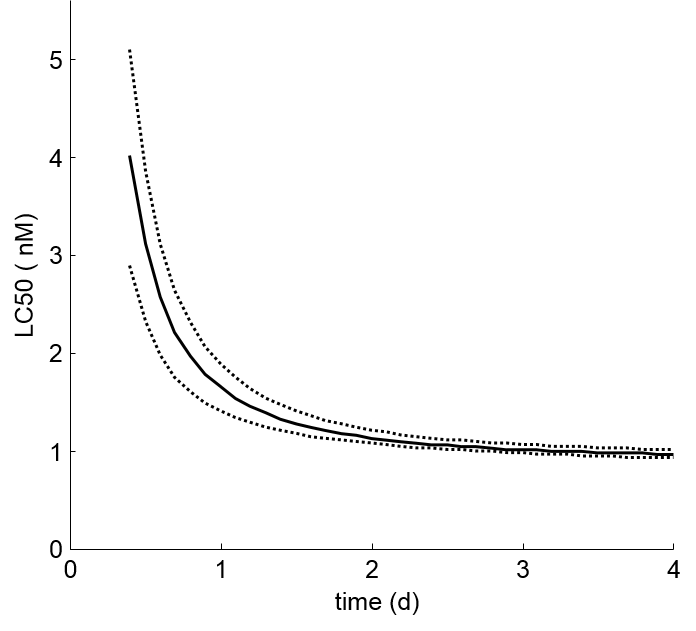
  • Model parameters can be used to predict LCx,t (with confidence interval) for any effect fraction x and any exposure duration t (extrapolation to non-tested exposure durations is thus possible).
  • Model parameters can be used to predict mortality (with confidence interval) for any exposure profile (e.g., profiles resulting from monitoring data or fate models).
  • The method can also be used to analyse or to predict the effects of multiple stressors (mixtures of toxicants, or the combination of chemical and non-chemical stressors).
Dr. Tjalling Jager (one of the developers of GUTS) acts as an advisor for these activities of Bongers EcoTox Services.

A practical example

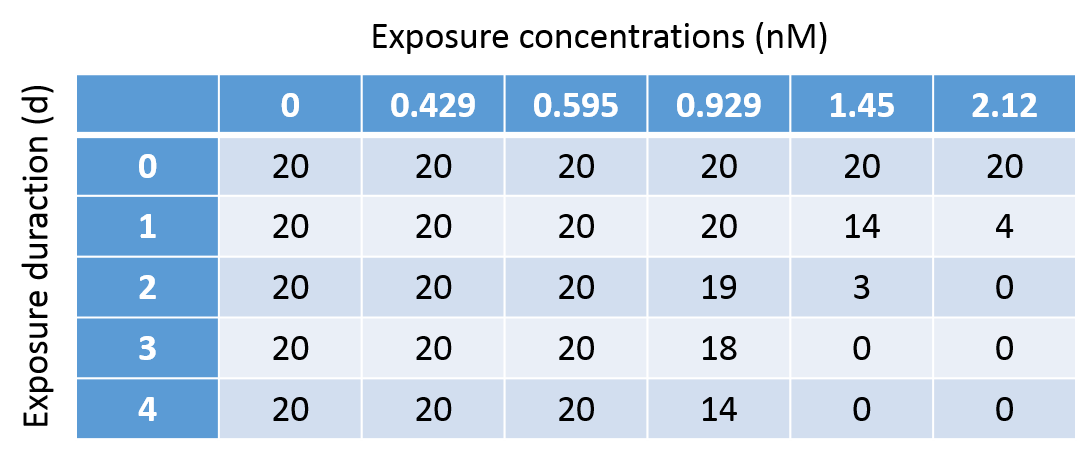
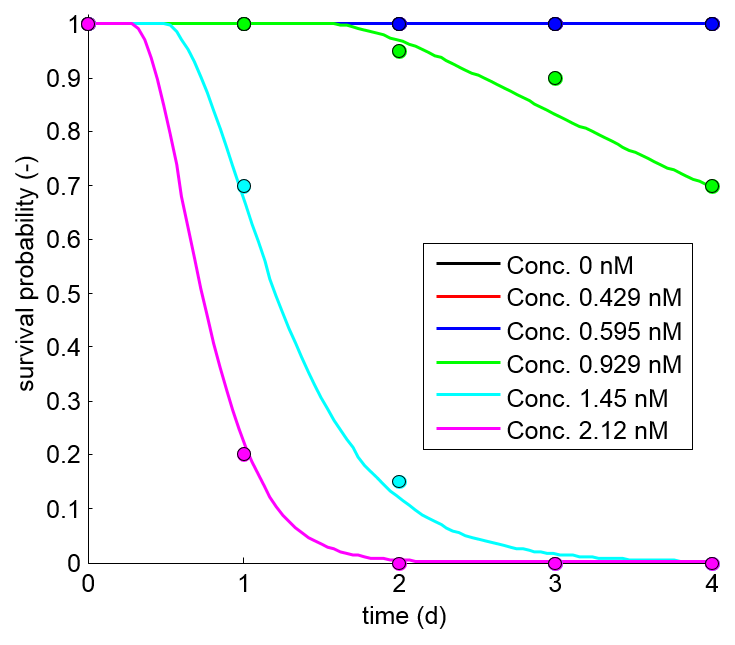
The advantages of the GUTS-approach are most easily demonstrated by an example analysis on a typical data set. The data used here are for the insecticide fenvalerate in fathead minnows (Pimephales promelas). The test design includes 6 treatments (including a control) with 20 individuals per treatment, and 4 days at which survival is scored. Normally, only the results on day 4 are used to calculate an LC50 (which is problematic here as there is only a single treatment with partial mortality).
 
Data source: Geiger, D.L., Brooke, L.T., Call, D.J. (1990). Acute toxicities of organic chemicals to fathead minnows (Pimephales promelas) Volume V. Center for Lake Superior Environmental Studies, University of Wisconsin-Superior, USA
These data can be analysed with GUTS. Here, the fit is made with the special case of the "hazard model with scaled internal concentrations" (identical to the method as described in the ISO and OECD guidances). Left the fit to the data set, and right the 4 fitted parameters with their confidence intervals.
 
The no-effect concentration (or NEC) should be seen as the concentration that has no effect on mortality, even after prolonged exposure (of course under the assumption that the model is correct). The "elimination rate" determines the rate at which the internal concentration in the animal equilibrates with the concentration in the medium (the rate is a combination of the toxicokinetic elimination and possible transformation processes and receptor and damage kinetics).

The model parameters can now be used to generate a number of predictions. For example for the LC50 versus time (with 95% confidence interval), and even for the LC50 after 8 days (an extrapolation based on the estimated parameters).
 
The LC50 depends on time, and after prolonged exposure, the value will approach the no-effect concentration (the "incipient LC50" thus equals the NEC). In this case, the LC50 rapidly approaches the ultimate value, caused by the relatively high value of the elimination rate. The value for the standard 4d-LC50 is determined with greater precision than with a standard dose-response analysis as all data are used in the process.

The parameters can also be used to predict mortality as a consequence of a specific exposure pattern (e.g., the results of a fate model). The prediction hinges on the assumption that the model is correct, and is only relevant for the specific other conditions in the test (temperature, lack of food, species and size of fish, etc.). As an example, below a prediction of the mortality (right, with 95% confidence interval) as a result of an exposure scenario with two pulses (left) of fenvalerate.

Scientific literature, selection:

  • Ashauer R, Wittmer I, Stamm C and Escher BI (2011). Environmental risk assessment of fluctuating diazinon concentrations in an urban and agricultural catchment using toxicokinetic-toxicodynamic modeling. Environ Sci Technol 45 (22):9783-9792. DOI 10.1021/es202413a
  • Ashauer R, Thorbek P, Warinton JS, Wheeler JR and Maund S (2013). A method to predict and understand fish survival under dynamic chemical stress using standard ecotoxicity data. Environ Toxicol Chem 32(4):954-965. DOI 10.1002/etc.2144
  • Jager T, Albert C, Preuss TG, Ashauer R (2011). General Unified Threshold model of Survival - a toxicokinetic-toxicodynamic framework for ecotoxicology. Environ Sci Technol 45:2529-2540. DOI 10.1021/es103092a
  • Jager T (2014). Reconsidering sufficient and optimal test design in acute toxicity testing. Ecotoxicology 23(1):38-44. DOI 10.1007/s10646-013-1149-7
An extensive list of publications on survival modelling and GUTS can be found on DEBtox.info.


Bongers EcoTox Services, www.bongers-ets.nl, Chamber of Commerce 62404563